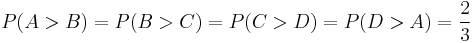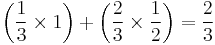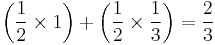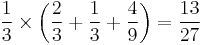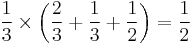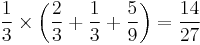Nontransitive dice
A set of nontransitive dice is a set of dice for which the relation "is more likely to roll a higher number" is not transitive. See also intransitivity.
This situation is similar to that in the game Rock, Paper, Scissors, in which each element has an advantage over one choice and a disadvantage to the other.
Contents |
Example
Consider a set of three dice, A, B and C such that
- die A has sides {2,2,4,4,9,9},
- die B has sides {1,1,6,6,8,8}, and
- die C has sides {3,3,5,5,7,7}.
Then:
- the probability that A rolls a higher number than B is 5/9 (55.55 %),
- the probability that B rolls a higher number than C is 5/9, and
- the probability that C rolls a higher number than A is 5/9.
Thus A is more likely to roll a higher number than B, B is more likely to roll a higher number than C, and C is more likely to roll a higher number than A. This shows that the relation "is more likely to roll a higher number" is not transitive with these dice, and so we say this is a set of nontransitive dice.
Efron's dice
Efron's dice are a set of four nontransitive dice invented by Bradley Efron.
The four dice A, B, C, D have the following numbers on their six faces:
- A: 4, 4, 4, 4, 0, 0
- B: 3, 3, 3, 3, 3, 3
- C: 6, 6, 2, 2, 2, 2
- D: 5, 5, 5, 1, 1, 1
Probabilities
Each die is beaten by the previous die in the list, with a probability of 2/3:
B's value is constant; A beats it on 2/3 rolls because four of its six faces are higher.
Similarly, B beats C with a 2/3 probability because only two of C's faces are higher.
P(C>D) can be calculated by summing conditional probabilities for two events:
- C rolls 6 (probability 1/3); wins regardless of D (probability 1)
- C rolls 2 (probability 2/3); wins only if D rolls 1 (probability 1/2)
The total probability of win for C is therefore
With a similar calculation, the probability of D winning over A is
Best overall die
The four dice have unequal probabilities of beating a die chosen at random from the remaining three:
As proven above, die A beats B two thirds of the time but beats D only one third of the time. The probability of die A beating C is 4/9 (A must roll 4 and C must roll 2). So the likelihood of A beating any other randomly selected die is:
Similarly, die B beats C two thirds of the time but beats A only one third of the time. The probability of die B beating D is 1/2 (only when D rolls 1). So the likelihood of B beating any other randomly selected die is:
Die C beats D two thirds of the time but beats B only one third of the time. The probability of die C beating A is 5/9. So the likelihood of C beating any other randomly selected die is:
Finally, die D beats A two thirds of the time but beats C only one third of the time. The probability of die D beating B is 1/2 (only when D rolls 5). So the likelihood of D beating any other randomly selected die is:
Therefore the best overall die is C with a probability of winning of 0.5185.
Variants with equal averages
Note that Efron's dice have different average rolls: the average roll of A is 8/3, while B and D each average 9/3, and C averages 10/3. The non-transitive property depends on which faces are larger or smaller, but does not depend on the absolute magnitude of the faces. Hence one can find variants of Efron's dice where the odds of winning are unchanged, but all the dice have the same average roll. For example,
- A: 6, 6, 6, 6, 0, 0
- B: 4, 4, 4, 4, 4, 4
- C: 8, 8, 2, 2, 2, 2
- D: 7, 7, 7, 1, 1, 1
or
- A: 7, 7, 7, 7, 1, 1
- B: 5, 5, 5, 5, 5, 5
- C: 9, 9, 3, 3, 3, 3
- D: 8, 8, 8, 2, 2, 2
These variant dice are useful, e.g., to introduce students to different ways of comparing random variables (and how only comparing averages may overlook essential details).
Numbered 1 through 24 dice
A set of four dice using all of the numbers 1 through 24 can be made to be nontransitive. With adjacent pairs, one die will win approximately 2 out of 3 times.
For rolling high number, B beats A, C beats B, D beats C, A beats D.
A: 1, 2, 16, 17, 18, 19B: 3, 4, 5, 20, 21, 22C: 6, 7, 8, 9, 23, 24D: 10, 11, 12, 13, 14, 15
Relation to Efron's dice
These dice are basically the same as Efron's dice, as each number of a series of successive numbers on a single die can all be replaced by the lowest number of the series and afterwards renumbering them.
A: 1, 2, 16, 17, 18, 19 -> 1, 1, 16, 16, 16, 16 -> 0, 0, 4, 4, 4, 4B: 3, 4, 5, 20, 21, 22 -> 3, 3, 3, 20, 20, 20 -> 1, 1, 1, 5, 5, 5C: 6, 7, 8, 9, 23, 24 -> 6, 6, 6, 6, 23, 23 -> 2, 2, 2, 2, 6, 6D: 10, 11, 12, 13, 14, 15 -> 10, 10, 10, 10, 10, 10 -> 3, 3, 3, 3, 3, 3
Miwin's dice
Miwin's Dice were invented in 1975 by the physicist Michael Winkelmann.
Consider a set of three dice, III, IV and V such that
- die III has sides 1, 2, 5, 6, 7, 9
- die IV has sides 1, 3, 4, 5, 8, 9
- die V has sides 2, 3, 4, 6, 7, 8
Then:
- the probability that III rolls a higher number than IV is 17/36
- the probability that IV rolls a higher number than V is 17/36
- the probability that V rolls a higher number than III is 17/36
Three-dice set with minimal alterations to standard dice
The following intransitive dice have only a few differences compared to 1 through 6 standard dice:
- as with standard dice, the total number of pips is always 21
- as with standard dice, the sides only carry pip numbers between 1 and 6
- faces with the same number of pips occur a maximum of twice per die.
- only two sides on each die have numbers different from standard dice:
- A: 1, 1, 3, 5, 5, 6
- B: 3, 2, 3, 4, 5, 4
- C: 1, 2, 2, 4, 6, 6
Like Miwin’s set, the probability of A winning versus B (or B vs. C, C vs. A) is 17/36. The probability of a draw, however, is 4/36, so that only 15 out of 36 rolls lose. So the overall winning expectation is higher.
Freivalds's investigation
The set of nontransitive dice were investigated by the Latvian computer scientist and mathematician Rusins Freivalds. He showed that if there is a set of n dice, and each die beats the next with probability p, then p can be arbitrary close (but not equal) to 3/4 = 0.75 when n goes to infinity.
Warren Buffett
Warren Buffett is known to be a fan of nontransitive dice. In the book Fortune's Formula: The Untold Story of the Scientific Betting System that Beat the Casinos and Wall Street, a discussion between him and Edward Thorp is described. Buffett and Thorp discussed their shared interest in nontransitive dice. "These are a mathematical curiosity, a type of 'trick' dice that confound most people's ideas about probability."
Buffett once attempted to win a game of dice with Bill Gates using nontransitive dice. "Buffett suggested that each of them choose one of the dice, then discard the other two. They would bet on who would roll the highest number most often. Buffett offered to let Gates pick his die first. This suggestion instantly aroused Gates's curiosity. He asked to examine the dice, after which he demanded that Buffett choose first."[1]
In 2010, Wall Street Journal magazine quoted Sharon Osberg, Buffett's bridge partner, saying that when she first visited his office 20 years earlier, he tricked her into playing a game with nontransitive dice that could not be won and "thought it was hilarious".[2]
See also
References
- ^ "Bill Gates speaks: insight from the world's greatest entrepreneur - Bill Gates, Janet Lowe". Books.google.ie. http://books.google.ie/books?id=Qoho6AIXTksC&pg=PA148&dq=Buffet+suggested+that+each+of+them+choose+one+of+the+dice,+then+discard+the+other+two.+They+would+bet+on+who+would+roll+the+highest+number+most+often.+Buffet+offered+to+let+Gates+pick+his+dice+first.+This+suggestion+instantly+aroused+Gates%27s+curiosity.+He+asked+to+examine+the+dice,+after+which+he+demanded+that+Buffet+choose+first. Retrieved 2011-11-29.
- ^ "like-a-marriage-only-more-enduring: Personal Finance News from Yahoo! Finance". Finance.yahoo.com. 2010-12-06. http://finance.yahoo.com/career-work/article/111491/like-a-marriage-only-more-enduring?mod=career-leadership. Retrieved 2011-11-29.
- Gardner, Martin. The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems: Number Theory, Algebra, Geometry, Probability, Topology, Game Theory, Infinity, and Other Topics of Recreational Mathematics. 1st ed. New York: W. W. Norton & Company, 2001. 286-311.
- Bill Gates Bill Gates Speaks: Insight from the World's Greatest Entrepreneur